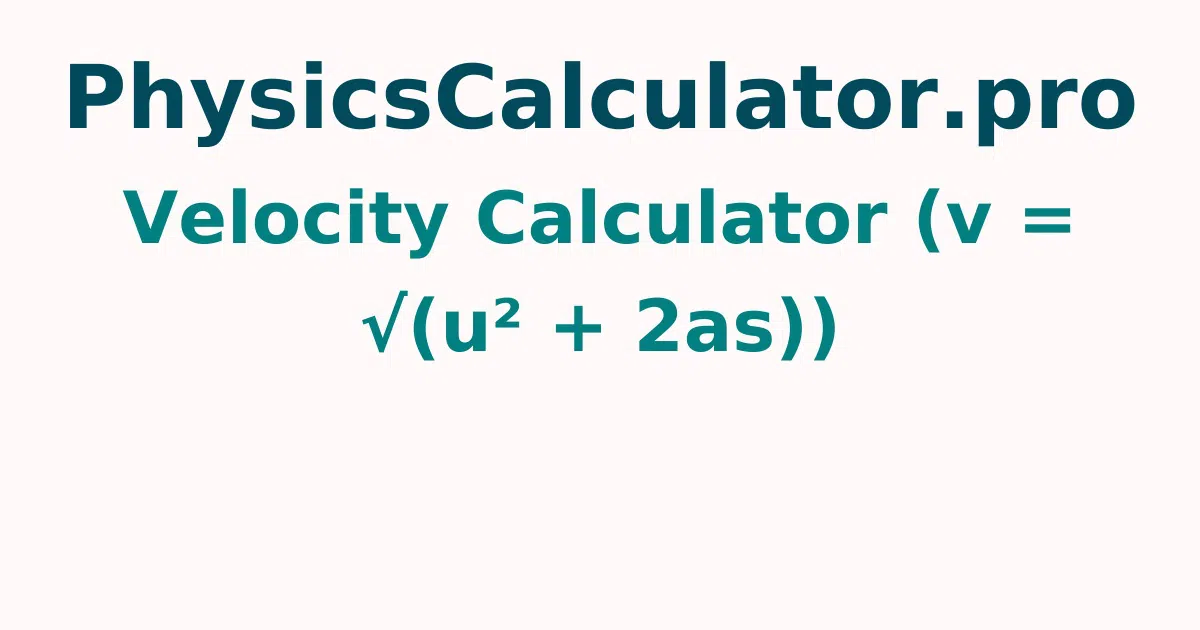Velocity Calculator (v = √(u² + 2as))

Velocity is defined as the rate at which an object's position changes as a function of time. It is a fundamental notion in classical mechanics that deals with the motion of objects.

The formula for Calculating Final Velocity: When you have initial velocity, acceleration, and displacement, you can use this formula to compute the final velocity of a moving object.

v = √(u² + 2as)

• Where v = final velocity
• u = initial velocity
• a = acceleration and
• s = displacement

To get the final velocity value, carefully follow the easy procedures given below. The procedure is as follows

• First and foremost, you must determine the question's initial velocity, acceleration, and displacement.
• Multiply the acceleration and displacement by a factor of two.
• Double the result from the previous step.
• Add the above number to the squared initial velocity.
• To get the final velocity, take the square root of the resultant.

The following is the procedure on how to use the Velocity Calculator

• Fill in the appropriate input fields with the unknown's initial velocity, acceleration, displacement, and x.
• To obtain the result, select "Calculate the unknown" from the drop-down menu.
• Finally, the final velocity of an object will be displayed in the output field.

For more concepts check out physicscalculatorpro.com to get quick answers by using this free tool.

Example 1:

A car starts at a speed of 5 m/s and accelerates at a rate of 3 m/s^2 until it reaches a distance of 30 km from its starting position. What is the car's final velocity?

Solution:

Given Initial velocity u = 5 m/s

Acceleration a = 3 m/s^2

Displacement s = 30 km

Final velocity = ?

Convert displacement into meters

Displacement = 30 x 1000 = 30,000 meters

Final velocity v = √(u² + 2as)

By putting the given values we have v = √(5² + 2 x 3 x 30,000)

v = 424.2 m/s

Final velocity (v) = 424.2 m/s

Example 2:

Find the final velocity when the initial velocity is 12, acceleration is 9.7 and the distance covered is 42?

Solution:

Given Initial velocity u = 12 m/s

Acceleration a = 9.7 m/s^2

Displacement s = 42 km

Final velocity = ?

v = √(u² + 2as)

v = √(12² + (2 x 9.7 x 42))

v = 30.96 m/s

Hence, the final velocity is 30.96 m/s

1. What is velocity science, and how does it work?

The speed at which the position changes is called velocity. The displacement or position change (a vector quantity) per unit time is the average velocity.

2. What is the definition of final velocity in physics?

When gravity first exerts a force on an object, its initial velocity indicates how fast it travels. The final velocity, on the other hand, is a vector number that measures a moving body's speed and direction after it has reached its maximum acceleration.

3. What is an example of velocity?

The rate of motion, speed, or action is referred to as velocity. An automobile travelling at 75 miles per hour is an example of velocity. A moving body's speed and direction of motion. The quantity of velocity is a vector quantity.

4. Is work the same as velocity?

As a result, the work is unaffected by velocity or force. Newton's second law states that force is a function of mass and acceleration. The term "acceleration" refers to the rate at which something moves.

5. What is the definition of terminal velocity in water?

They can be expanded by boiling them for five minutes in water. Allowing them to fall freely in the air will bring them to a terminal velocity of around 30 cm. They act like raindrops in slow motion.